向量

向量是什么？

谈到线性代数，自然绕不开向量（vector）这个名词。那么你有没有思考过，向量究竟是什么？它有什么意义？

物理专业的同学，认为向量是力的一种表示，具有方向和大小两个特性。

计算机专业（图形学）的同学，认为向量是一个箭头，可以是平面中的箭头，也可以是空间中的一个箭头。

数学专业的同学，将向量看做是一组有序的数列。例如(x, y)和(x, y, z)，x、y、z之间的顺序不允许改变，这组数只要满足向量的加法与数乘即可（关于加法和数乘运算，后面会讲解）。

按照数学专业同学的说法，向量可表示的范围很广，例如用向量表示苹果的重量与价格的关系，x表示重量，y表示价格，x与y之间的次序固定，那么我们就可以得到一组苹果重量与价格关系的向量表示。

为了更好的理解教程后面的内容，希望你可以将向量看做是坐标系中的一个箭头，具有长度和方向两个特性，箭头的起始点在坐标系原点。

向量的模

我们用向量的模长表示向量的大小，即向量的长度，是一个标量。假设有向量v: (x, y)，可用|v|表示向量的模长，通过如下公式计算向量的模长。

向量的加法和减法

向量的加法，就是将两个向量对应位置的数相加，得到一个新的向量。

(x1, y1, ...) + (x1, y1, ...) = (x1 + x2, y1 + y2, ...) 

可以将向量看成空间中的一种运动，在二维平面中(3, 4), 表示向右（x正方向）运动3个单位，向上（y正方向）运动4个单位。

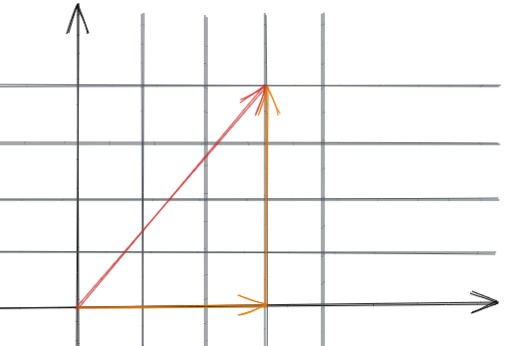
从(0, 0)点直接移动到(3, 4)点，与先从(0, 0)点移动到(3, 0)点，再移动到(3, 4)点的结果没有区别，所以有以下等式成立。

// 等式左边表示直接从(0, 0)点移动到(3, 4)点
// 等式右边表示先从(0, 0)点移动到(3, 0)点，再从(3, 0)点移动到(3, 4)点
(3, 4) = (3, 0) + (0, 4)

向量的减法，就是将两个向量对应位置的数相减，得到一个新的向量。

(x1, y1, ...) - (x1, y1, ...) = (x1 - x2, y1 - y2, ...) 

也可以看成空间中的一种运动，(3, 0) - (3, 4)表示点在(3, 0)点在向x轴负方向移动3个单位，再想y轴负方向移动4个单位，结果为(0, -4)。

向量的数乘

向量的数乘，就是将向量与一个数字标量进行乘法运算，结果是一个新的向量，结果向量的每一位等于原向量的每一位与数字标量相乘的结果。

scalar * (x1, y1, ...) = (x1 * scalar, y1 * scalar, ....)

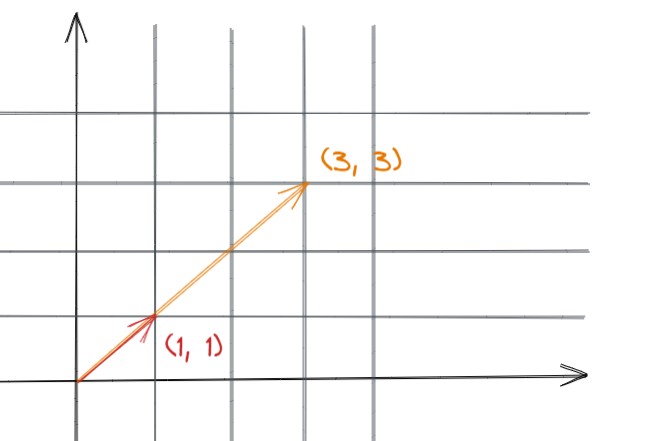
向量的数乘可以表示向量的长度的缩放，将向量v长度增长到3倍，但是方向保持不变，可以得到一个新的向量3v。

应用

线性代数这门课，始终围绕着向量的加法和数乘运算。在CG中，向量的加法用于计算模型的位移，向量的数乘用于计算模型的缩放。在后面，你会接触到更多向量的计算，但是加法和数乘始终是这门课程的核心。