坐标系

虽然国内的初高中数学对坐标系的介绍已经非常详细了，而且坐标系大家已经非常熟悉了，但是为了内容的完整性，我还是会专门用一节内容带大家回顾下坐标系的概念。也会详细讲解直角坐标系和极坐标系的适用情况。

概述

坐标系（coordinate system）是我们在学校中开始学习几何时，第一个学到的东西。它为几何图形学中所有的东西（包括点、线、面等）赋予了一个坐标，有了坐标系我们可以通过文字和语言来描述顶点的位置即顶点的坐标。

坐标系的种类有很多，常用的坐标系包括笛卡尔坐标系、平面极坐标系（简称极坐标系）、柱坐标系和球坐标系。不同的坐标系，虽然作用都是定位平面（或空间）上的某个顶点，但是在不同情况下使用合适的坐标系会极大简化计算的复杂度，例如我们想要计算平面上某一点在绕原点旋转一定角度后的顶点坐标，采用极坐标系会很方便的计算出结果，而处理计算某一点平移后的点时，采用直角坐标系会更方便计算。在本节的后面我会向大家详细介绍，笛卡尔坐标系和极坐标系。

你还可以自己定义一种坐标系，只要平面（或者空间）上的每个顶点都有一个唯一的坐标即可。

笛卡尔坐标系

在教程首页展示的两个坐标系模型就是笛卡尔坐标系，也称直角坐标系。

二维笛卡尔坐标系用来描述平面上的某一点的位置，包含一个主轴（后面称X轴）和纵轴（后面称Y轴），通常情况下X轴是水平方向的，从左指向右，Y轴是竖直方向的，从下指向上，X轴和Y轴的交点，称为该坐标系的原点（用O表示）。

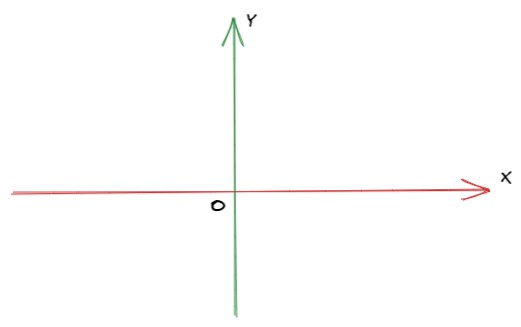
假设平面中有一点A，A在X轴方向上的投影为Ax，A在Y轴上的投影Ay，Ax到原点O的距离为a，Ay到原点O的距离为b，那么点A的坐标为（a，b）。

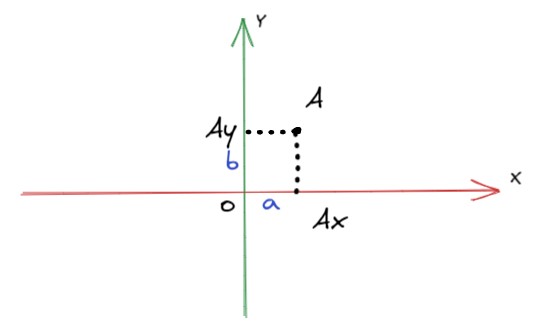
扩展到三维，只需要在二维直角坐标系的基础上再添加一个坐标轴——Z轴，通常情况下，X轴、Y轴、Z轴是互相垂直的，但是可以通过一系列的变换，变成非垂直的情况（后面我会详细介绍坐标系变换的内容）。

三维坐标系中顶点的坐标由三个分量组成(x, y, z)，x和y的意义与二维坐标系的x、y相同，z类似，表示顶点在Z轴的投影点到原点的距离。

谈论到三维直角坐标系，经常会区分左手坐标系和右手坐标系。

在三维坐标中，根据Z轴(深)的不同方向，分为“右手系”和“左手系”两种坐标系。当轴的方向是（在一般二维直角坐标系上：向右为X轴，向上为Y轴）从眼前伸向深处时，该坐标系是左手系，反之则是右手系。

你一定见过类似如下的图。

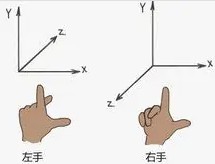图片来自百度百科

这是用来区分左手系和右手系的一种方式。

• 右手的拇指表示X轴
• 食指表示Y轴
• 中指表示Z轴

关于更多区分左手系和右手系的方法，这里不做介绍了，你可以在网上搜索。

计算顶点平移后的坐标

前面说过笛卡尔坐标系，在确定顶点平移后的位置时非常有用。假设平移前顶点坐标为(x, y)，顶点向X正轴方向平移了3个单位，向Y轴正轴方向平移了4个单位，那么平移后的坐标，很显然为(x + 3, y + 4)，是不是很简单，但是如果你用其他类型的坐标系来计算平移，可能会非常复杂。

计算坐标平移非常简单，那当计算旋转时，怎么办呢？例如在平面上，当有一点A绕原点O旋转45度，那么如何计算旋转后A点的坐标。

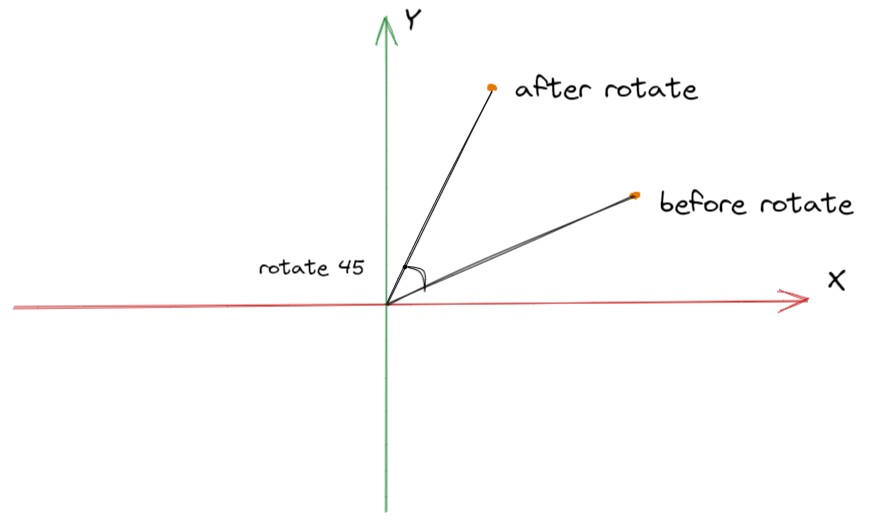
你可以在草稿本上尝试计算下旋转后的坐标。

其实当处理旋转时，使用极坐标比笛卡尔坐标更加方便，下面我们一起看一看极坐标。

极坐标系

极坐标属于二维坐标系统，创始人是牛顿。在平面内取一点O，叫极点，引一条射线OX，叫做极轴，经过O点画一条线段OA，OA与极轴有一个夹角$\theta$，OA的长度为l，那么此时A点的极坐标为:

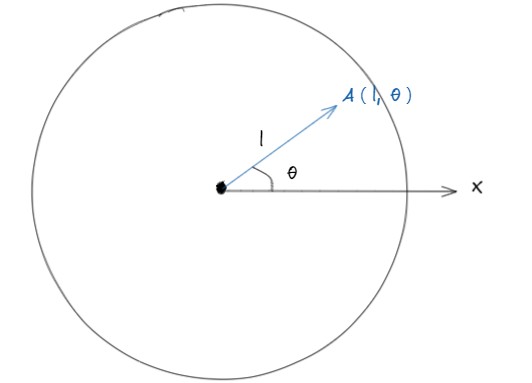
极坐标系的定义十分简单。一般情况下，极轴由极点O水平向右，角度的正方向极轴的逆时针方向，但是你可以将极轴定义成任意方向，并且角度的正方向可以是逆时针也可以是顺时针。

极坐标在旋转中的应用

由于极坐标的定义由长度和角度定义(length, angle)，所以在计算旋转时十分方便，例如极坐标点$（l,\theta ）$旋转$\alpha$角度后，坐标为$（l,\theta + \alpha ）$。

可能有的人会问了，平时我们用的都是笛卡尔坐标系，那么如何计算笛卡尔坐标系中的某个点，旋转$\alpha$角度后的笛卡尔坐标系呢？

其实，只需要将笛卡尔坐标系转化成极坐标，然后将极坐标的角度值进行加减得到旋转后的极坐标，最后再转换成笛卡尔坐标系即可。

而笛卡尔和极坐标的转换十分简单，只需要利用简单的三角函数即可计算，你可以尝试自己在草稿本上计算。下面我直接给出图解计算过程。

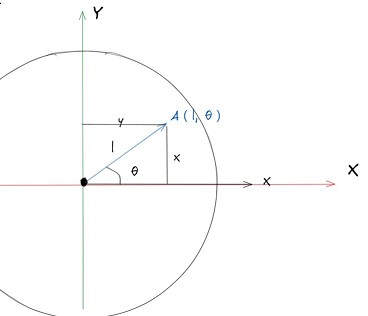
如图，点A的极坐标为$（l,\theta ）$，所以OA的长度为l，AOX的角度为$\theta$，由三角函数很容易得到x和y的值。

从笛卡尔坐标系转换为极坐标，即通过x和y，求l和$\mathit{\theta }$。

极坐标对于求解旋转相关的问题十分方便，我在矩阵证明（一）中计算旋转矩阵中，就用到了极坐标。