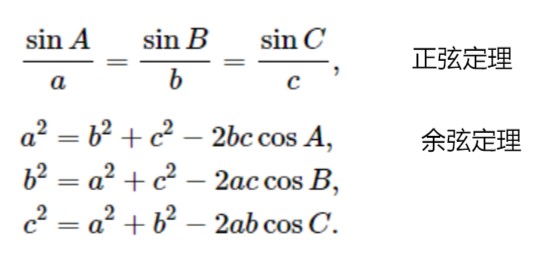三角函数

三角函数（trig functions），大家应该都不会陌生，想到三角函数，脑子里就会出现sin、cos、tan等词语，和一系列难以记忆的公式。虽然严格来说三角函数并不属线性代数这门学科，但是它在图形学中出现的频次实在太高了，所以不得不将其在这里介绍一下（写到这时，我正在想《你好，线性代数》这门教程的名字是否合适，不过暂时就这样吧）。

一. 基本三角函数

有一个直角三角形，如下。

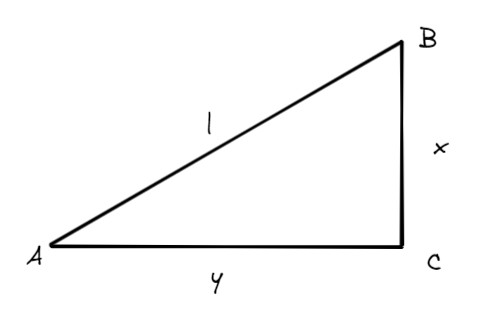
三角形的三个角为A、B、C，直角边长为x和y，斜边长为l。

1. 正弦函数（sine ）

正弦函数，等于与角对应的直角边长除以斜边长，以角A为例。

$\sin \left(A\right) = \frac{x}{l}$

2. 余弦函数（cosine）

余弦函数，等于与角相邻的直角边长除以斜边长，以角A为例。

$\cos \left(A\right) = \frac{y}{l}$

3. 正切函数（tangent）

正切函数，等于与角对应的直角边长除以与角相邻的直角边长，以角A为例。

$\tan \left(A\right) = \frac{x}{y}$

4. 正割函数（secant）

正割函数，与余弦函数相反，等于斜边长除以与角相邻的直角边长。

$\sec \left(A\right) = \frac{l}{x} = \frac{1}{\cos \left(A\right)}$

5. 余割函数（cosecant）

余割函数，与正弦函数相反，等于斜边长除以与角对应的直角边长。

$\csc \left(\mathrm{A}\right) = \frac{l}{y} = \frac{1}{\sin \left(A\right)}$

6. 余切函数（cotangent）

余切函数，与正切函数相反，等于与角相邻的直角边长除以与角对应的直角边长。

$\cot \left(A\right) = \frac{y}{x} = \frac{1}{\tan \left(A\right)}$

二. 延伸公式

我们用单位圆来推导三角函数，单位圆就是半径为1的圆。如图有一个单位圆，原点为O，半径为1，有一条半径OA，A点的坐标为(x, y)，OA与x轴的夹角为$\theta$。

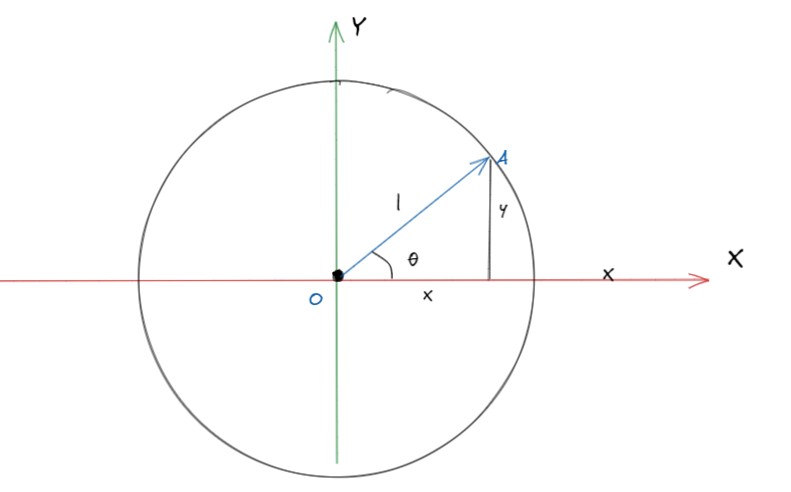
1. 平方公式 我们知道勾股定理。

在一个直角三角形中，两个直角边的平方和等于斜边长的平方。

所以将勾股定理带入到上图的单位圆中，得到：

${\chi }^2 + y^2 = 1$

因为，斜边长为1，所以有以下等式成立。

$\cos \left(\mathrm{\theta }\right) = \mathcal{x}$
$\sin \left(\mathrm{\theta }\right) = \mathrm{y}$

代入勾股定理，可以得到以下公式。

${\sin }^2\left(\mathrm{\theta }\right) + co{s}^2\left(\mathrm{\theta }\right) = 1$

通过同样的代入方式，我们也可以得到其他平方公式。

$1 + ta{n}^2\left(\mathrm{\theta }\right) = se{c}^2\left(\mathrm{\theta }\right)$
$1 + {\mathit{cot}}^2\left(\mathrm{\theta }\right) = \mathrm{c}s{c}^2\left(\mathrm{\theta }\right)$

2. 对称公式

根据圆的对称性，有以下等式成立。

$\sin (-\mathrm{\theta }) = -sin\left(\mathrm{\theta }\right)$
$\cos \left(-\mathrm{\theta }\right) = \mathit{cos}\left(\mathrm{\theta }\right)$
$\tan \left(-\mathrm{\theta }\right) = -\mathit{tan}\left(\mathrm{\theta }\right)$
$\sin \left(\frac{\mathrm{\pi }}{2} - \mathrm{\theta }\right) = \cos \left(\mathrm{\theta }\right)$
$\cos \left(\frac{\mathrm{\pi }}{2} - \mathrm{\theta }\right) = \sin \left(\mathrm{\theta }\right)$
$\tan \left(\frac{\mathrm{\pi }}{2} - \mathrm{\theta }\right) = \cot \left(\mathrm{\theta }\right)$

3. 和差公式

下面的恒等式涉及对两个角的和或差取三角函数:

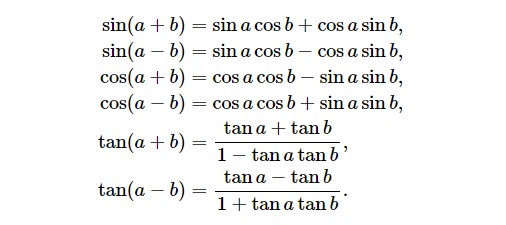
4. 二倍角公式

下面的公式可以将二倍角转换为单倍角。

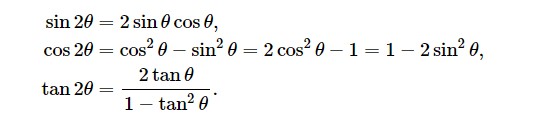
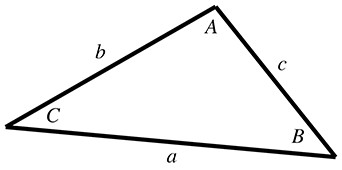
5. 正弦定理和余弦定理

在已知边长和角度时，求解另一个未知边长或者角度时，可以使用正弦定理和余弦定理。